I teach 7th and 8th grade math and I recently noticed that my students were becoming reliant on me to help them understand complex math tasks. I teach the English Learner classes at my school and often times I translate instructions into Spanish to ensure students understand the prompts. I also routinely summarize what the math prompts are asking them to do. Unfortunately this has led to students waiting for me to explain the prompt and many do not bother to read the prompt as a result. At the beginning of the year, my school administered the Star Math Renaissance assessment to students to determine baseline math ability. One of my EL 1 students took the test in English as instructed. He was very disappointed with his score and was adamant that the test did not reflect his ability so he retook the test in Spanish. His score jumped from grade equivalent 5.0 to 8.8.

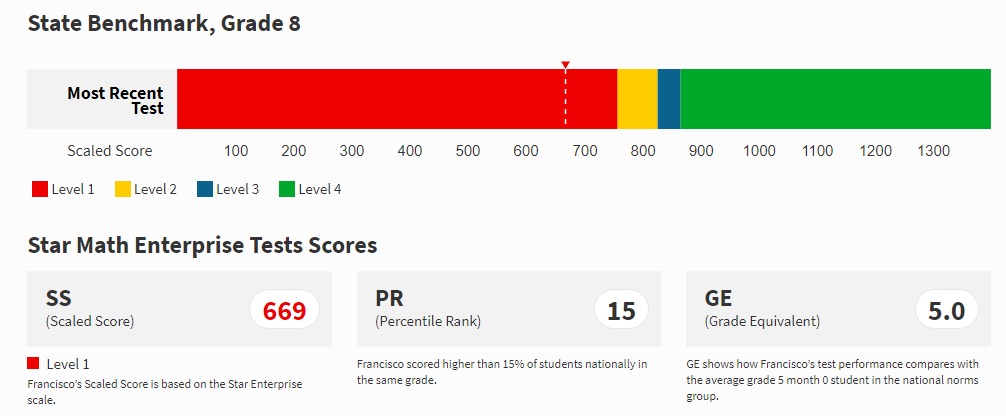
He took the same test and the only thing that changed was his ability to understand the questions being asked of him. He had made a powerful point: this is what I can do when I know what to do. Yes, this can be frustrating for students but we must remember that our students will be asked to take standardized math test in English (with the exception of newcomers) therefore we should be equipping them with the skills they need to decipher complex math tasks in English. This point became even clearer to me when my students recently took an assessment and many gave these types of answers:

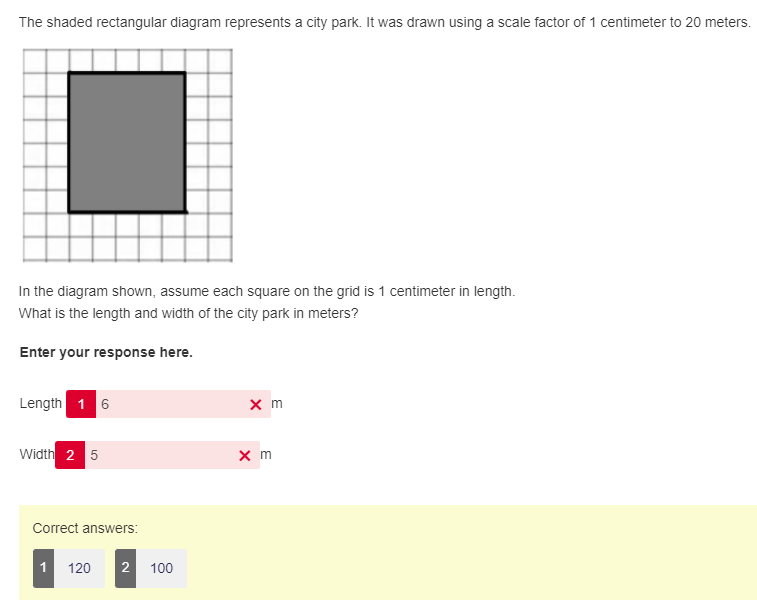
Now, clearly this student got the answer wrong however it is possible they misunderstood what was being asked. They were not asked directly to convert the length and width of the scaled drawing of the park, this had to be inferred by reading the question: “What is the length and width of the city park in meters?” To fully understand what to do here, students would need to be able to identify the information that shows 1 unit on the grid is equivalent to 1 centimeter. Then they would have to understand that they are being asked for a quantity in meters rather than centimeters to then use the provided scale to convert their answers. If students don’t know how to identify this important information, they may not be able to fully show their understanding.

Now in this example, it is clear that this student understands congruency. This student is attempting to prove congruency without realizing that the initial statement already establishes that the figures are congruent. As a result of this misunderstanding, it is not possible to say with certainty that this student can or cannot explain which transformations they used to get from figure a to figure b. Of course, on standardized tests students are not given the benefit of the doubt and this response is simply marked wrong.

Without me to elaborate on what exactly they were being asked to do, the answers of my students reveal they misunderstood the directions on many occasions. Of course, my instinct is that there would be fewer such mistakes if they fully understood the prompt but I can’t prove that. What I can do though moving forward is ensure I help students develop their ability to read complex math prompts to avoid confusion in the future. This is where the Three Reads Math Language Routine comes in. The Math Language Routines were developed at at Stanford University (a summary can be found here) and provide ways to support students as they are asked to understand complex math prompts and communicate their responses to these prompts. The main premise is that “students do not need to understand a language completely before they can start making sense of academic content and negotiate meaning in that language.” As a result, the language routines are “well-suited to the meet the needs of linguistically and culturally diverse students who are simultaneously learning mathematics while acquiring English.” This means that in addition to providing translations to the EL1 student from above, I need to also ensure he is learning how to navigate complex math tasks in English. Here is a short summary of the Three Reads math language routine:

Purpose

To ensure that students know what they are being asked to do, create opportunities for students to reflect on the ways mathematical questions are presented, and equip students with tools used to actively make sense of mathematical situations and information (Kelemanik, Lucenta, & Creighton, 2016). This routine supports reading comprehension, sense-making, and meta-awareness of mathematical language. It also supports negotiating information in a text with a partner through mathematical conversation.

How it happens

In this routine, students are supported in reading a mathematical text, situation, or word problem three times, each with a particular focus. The intended question or main prompt is intentionally withheld until the third read so that students can concentrate on making sense of what is happening in the text before rushing to a solution or method.

Read #1: Shared Reading (one person reads aloud while everyone else reads with them) The first read focuses on the situation, context, or main idea of the text. After a shared reading, ask students “what is this situation about?” This is the time to identify and resolve any challenges with any non-mathematical vocabulary. (1 minute)

Read #2: Individual, Pairs, or Shared Reading After the second read, students list any quantities that can be counted or measured. Students are encouraged not to focus on specific values. Instead they focus on naming what is countable or measurable in the situation. It is not necessary to discuss the relevance of the quantities, just to be specific about them (examples: “number of people in her family” rather than “people,” “number of markers after” instead of “markers”). Some of the quantities will be explicit (example: 32 apples) while others are implicit (example: the time it takes to brush one tooth). Record the quantities as a reference to use when solving the problem after the third read. (3–5 minutes)

Read #3: Individual, Pairs, or Shared Reading During the third read, the final question or prompt is revealed. Students discuss possible solution strategies, referencing the relevant quantities recorded after the second read. It may be helpful for students to create diagrams to represent the relationships among quantities identified in the second read, or to represent the situation with a picture (Asturias, 2014). (1–2 minutes).

Here is a video of me introducing three reads to one of my 7th grade classes:

This is the prompt the students were working on:

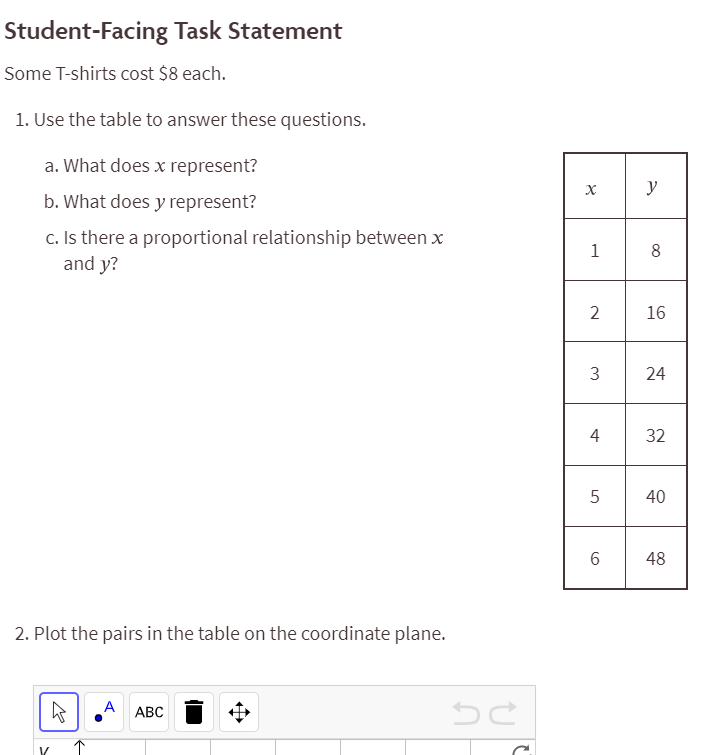
Here is a video of me introducing three reads to one of my 8th grade classes:

This is the prompt the students were working on:

Notice how the focus was on the text rather than on me telling students what to do which teaches students how to identify the information in the given prompt they need to successfully respond to the task. This was my first time implementing the Three Reads math language routine and the results so far have been very good. In my 8th grade class from the above video, 100% of students were able to show their understanding of the prompt as evidenced by their ability to identify congruent corresponding angles and/or scale factors to take one figure to the other. Also, I didn’t have any students ask for help because they “didn’t get it.” Since everyone was reading along as the class was breaking down the problem together, the task became very clear to everyone. It wasn’t captured on the video but I also had students draw a t-shirt and a dollar sign to further help them understand the proportional relationship given in the 7th grade math task which was especially helpful for my EL1s and EL2s. I plan to continue using this math language routine in my classes to ensure students further develop their ability to understand complex math tasks.

Fortunately, the Three Reads math language routine appears throughout the open up resources course guide (Download for free at openupresources.org) as a support for English Language Learners (look for the big blue boxes):

The Three Reads math language routine can be found under the launch portions of the OUR lessons listed below but of course can be adapted as needed:

Activity Title	Grade	Unit	Lesson
Concert Tickets	6	2	10
A Trip to the Aquarium	6	2	16
Climbing the Burj Khalifa	6	3	1
Cheesecake, Milk, and Raffle Tickets	6	3	6
Picnics on the Rail Trail	6	3	8
How Much It Costs to Paint	6	3	17
Fractional Batches of Ice Cream	6	4	7
How Many Would it Take? (Part 2)	6	4	13
Determining Shipping Costs (Part 1)	6	4	17
Decimals All Around	6	5	4
Distance between Hurdles	6	5	14
Choosing Equations to Match Situations	6	6	4
Partitioned Rectangles When Lengths are Unknown	6	6	10
Calculating Surface Area	6	6	14
Making a Banner	6	6	18
Above and Below Zero	6	7	1
Diego’s Bake Sale	6	7	16
Prizes on Grand Opening Day	6	7	17
More Factors and Multiples	6	7	18
Best Restaurant	6	9	4
Making Bread Dough	7	2	2
Revisiting Bread Dough	7	2	4
Recycling	7	2	6
Cost of a Stained-Glass Window	7	3	11
Shopping in Two Different Cities	7	4	10
A Car Dealership	7	4	11
Saw Mill	7	4	15
Winter Temperatures	7	5	2
Solar Power	7	5	7
Multiplication and Division	7	5	11
Water Level in the Aquarium	7	5	12
Buying and Selling Power	7	5	14
Trip to the Mountains	7	5	15
Entrance Fees	7	6	1
Even More Situations, Diagrams, and Equations	7	6	6
A Sale on Shoes	7	6	12
Elevator	7	6	17
Different Scales	8	3	2
Summer Reading	8	3	6
Payback Plan	8	3	9
Apples and Oranges	8	3	12
Elevators	8	4	9
A Close Race	8	4	11
Dimes and Quarters	8	5	3
Shadows	8	5	9
Hemispheres in Boxes	8	5	19
Cutting Corners	8	8	10
The Screen Is the Same Size . . . Or Is It?	8	8	16